解一元二次不等式的图象法说课稿

字号：T|T

解一元二次不等式的图象法（1）说课

教材:中等职业教育国家规划教材数学（基础版）第一册P118～121

【教材分析】

1．教材的地位和作用：

解一元二次不等式是数学学习和研究的重要工具，数学以简洁为美，如何能准确迅速的解各种类型的一元二次不等式呢？这就要求学生熟练掌握各种常见的解法，并能根据被解一元二次不等式的类型结合每种解法的特点，择简而用。学生已经掌握了因式分解法，本节课讲授的是一元二次不等式的图象法(1)，主要解决对应的二次函数与坐标轴有两个交点时，如何根据图象解不等式。下一节将解决对应的二次函数与坐标轴有一个交点和没有交点时，如何根据图象解不等式同时加强练习。

2．教学内容:

本节课讲授的是一元二次不等式的图象法(1). 学生对一元二次方程、一元二次不等式与二次函数这些基本内容都比较熟悉,但是,初中数学并没有专门讲述相关解法.教学时,先复习这些内容,进一步加深学生对二次函数的性质和图象的理解,接着介绍“图象法”这一概念,引导学生利用二次函数的图象和一元二次方程来解一元二次不等式,并理解它们三者之间的内在联系.

3．教学重、难点:

教学重点是如何利用二次函数的图象来求解一元二次不等式,教学难点是理解一元二次不等式与一元二次方程、二次函数的关系.

【目标分析】

依据课程标准,结合学生的认知结构和年龄特点,从“知识与能力,教学过程与方法, 情感、态度、价值观”三个角度考虑,本节课确定以下教学目标.

目标层次	目标	目标分析
知识与能力目标	1.掌握二次函数的性质和图象; 2.能利用二次函数的图象与一元二次方程来求解一元二次不等式,理解它们三者之间的内在联系.	1.学生对二次函数的基本内容比较熟悉, 教学时,先复习这些内容,进一步加深学生对二次函数的性质和图象的理解,为学习新内容做铺垫. 2.这部分对学生而言,数与形是割裂的,没有真正和谐统一在一起,因此,运用传统的教学方法,学生很难理解,所以在教学中可使用多媒体课件辅助教学.利用动态多媒体课件的演示,启发、引导学生通过观察和分析图象的变化,主动思考,发现问题,解决问题,归纳总结出变化规律,掌握相关知识
教学过程与方法目标	培养“函数与方程”、“数形结合”数学思想	学生在数学思想上缺乏足够深度和广度,只有通过特定的数学活动,获得一些初步的经验,逐步形成较为完善的数学思想体系.
情感、态度、价值观目标	1.通过利用二次函数的图象求解一元二次不等式的解集, 培养学生关于、数形结合的数学思想; 2.通过研究函数、方程与不等式三者之间的内在联系,使学生认识到事物是相互联系、相互转化的,树立辨证的世界观.	1.学生的逻辑思维尚未完善,利用二次函数的图象求解一元二次不等式的解集有一定的难度,但好奇心十分活跃,模仿能力强,有强烈的求知欲. 2.函数、方程与不等式三者之间是有内在联系的, 数与形不是割裂的,而是和谐统一的.能否利用教材渗透人的学习品质的培养,是能否把新的教育理念落实到课堂的关键.

【教学过程分析】

1.整个教学过程按以下流程展开：

教学过程逻辑流程图

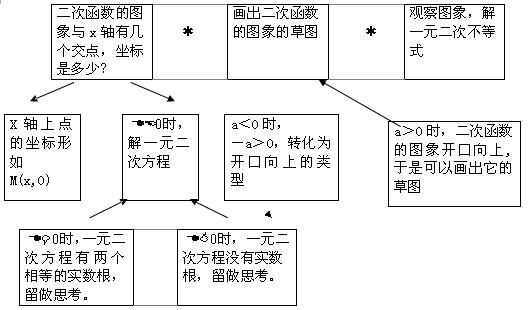
2．教学过程：
　　（1）新课引入
先复习提问“X轴上点的纵坐标是什么？”，接着直接给出一个简单的例子“求的图象与x轴的交点”，尽力调动绝大多数学生的积极性，引导学生由熟知的求二次函数的图象与x轴的交点的坐标开始主动的参与本节的学习。要求学生动手求交点。
　　（2）新课讲解
如果知道了的图象与x轴的交点,你能画出它的图象的草图吗?”要求学生自己试一试。进一步加深学生对二次函数的性质和图象的理解,为学习新内容做铺垫.给出具体的解答过程，充分发挥多媒体的优势，利用直观的点的移动和色段显示，引导学生观察图象，找到规律，最后指出这就是图象法。
　　（3）例题讲解
例题讲解是很重要的环节，引导学生一起作答。例（1）a＞0，并且对应的二次函数图象与x轴有两个交点时，解一元二次不等式。例（2）a＜0时，－a＞0，转化为开口向上的类型。
　　（4）小结
　　　　和学生一起将做题步骤加深印象，指出我们只要讨论的情况.
　　（5）练习用图象法解一元二次不等式
　　　　从a＞0和 a＜0两种题型，加强练习，

　　（6）思考
留以思考空间，激发学生强烈的求知欲，并为下一节作准备。根据学生的认知程度不同，留有选讲例题。
　　（7）作业布置
【教法、学法分析】
1．动（师生互动）：老师通过多媒体设计动画，让学生亲自动眼、动脑、动手参与教学活动，感悟知识的发生、发展过程。
2．变（灵活变式）：通过变式例题、习题，培养学生思维的广阔性和深刻性。
3．引（合理引导）：在教学中对思维受阻或某些学生容易产生歧义的地方，教师给以必要的引导，做到“引而不灌”，教师的引是为了学生的学。
　　4．渗（有机渗透）：渗透函数与方程、数形结合、化归等数学思想。
通过这四个方面师生双边活动，最终实现：激发学生学习的潜能，树立自信心，鼓励学生积极创新，落实课程标准，推进素质教育的实施。
【评价分析】
　　1．实现评价主体、评价方式的多样化，增加教学反馈层面。
在教学过程的各个环节中，把学生自我评价、教师评价结合起来，实现评价主体的多样化。课堂中采用口试、课堂观察、课后布置书面作业等各种评价方式，达到多层面的了解学生。
　　2．注重对学生学习过程的评价，促进学生的合作能力、创新能力。
在整个过程中，通过对学生参与教学活动的程度、自信心
合作交流的意识、以及独立思考的习惯、发现问题的能力进行评价，以激励性的语言促进他们合作，培养创新能力。
【教学设计说明】
　　1．指导思想
以推进素质教育的实施、落实课程标准为终极目标；以知识技能的形成、数学思维的完善和情感态度的发展为出发点；以多媒体为辅助教学手段；以教师的引导、参与为依托；以学生积极动手、动脑、动口为主线来构建本节教学模式。
2．设计思路
在以落实素质教育为宗旨，贯彻新教育理念为前提，从学生的认知特点出发，以师生互动交流为模式，把此节课设计成：
　　　（1）内容上：突出知识发生、发展的过程。
　　　（2）形式上：突出知识形成的必然性。
　　　（3）手段上：突出直观化的特点。
3．教材处理
认识到“教材是实现课程标准的具体体现”的前提下，认真体会教材编写者的意图，创造性的使用教材，使原来抽象的知识直观化、简单化。