一级建造师典型例题三

 例4.2 某地区1994—1999年间的住宅竣工面积情况如表4.4所示。按照最小平方法建立住宅竣工面积直线趋势模型，并将有关数据计算后填入表4.5。

解：　因 =6，=21， =555，= 2 087，=91， 故 =， ．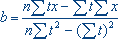

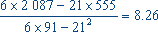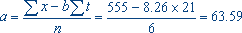表4.4　某地区住宅竣工面积资料

年份	时期序号（）	竣工面积（104 m 2）（）
1994	1	73
1995	2	80
1996	3	88
1997	4	95
1998	5	104
1999	6	115

所以，所求直线趋势方程为 .

以此方程预测2000年和2002年的住宅竣工面积， 分别取值为7和9。

2000年的住宅竣工面积预测值为

2000  = 63.59 + 8.26 × 7 = 121.41×10 4（ m 2），

同理                2002  = 63.59 + 8.26 × 9 = 137.93×10 4（ m 2）．

     表4.5　最小平方法确定模型参数计算表         单位: （１×10 4 m 2）

年   份	时期序号	竣工面积		2
1994	1	73	73	1
1995	2	80	160	4
1996	3	88	264	9
1997	4	95	380	16
1998	5	104	520	25
1999	6	115	690	36
合   计	21	555	087	91

例4.4 某企业为适应市场需求，要对新建水泥厂的规模作出决策。根据预测，新增的水泥需求量有三种可能：10×104 t，20×104 t，30×104 t。相应地也有三个方案，即新建水泥厂的规模可以分为10×104 t，20×105 t，30×104 t。根据技术资料以及有关原材料价格的核算，水泥厂建成后可获得的损益见表4.8。

表4.8　水泥厂规模决策表（一）              　　 单位：万元

	可能增加的年需求量			最大效益值
	10×104 t	20×104 t	30×104 t
建设规模10×104 t	100	100	100	100
建设规模20×104 t	0	300	300	300
建设规模30×104 t	－300	150	600	600
max{最大效益}=max{100，300，600}				600
优选的决策方案				建设规模30×104 t

表4.9  水泥厂规模决策表（二）      　　            单位：万元

	可能增加的年需求量			最小效益值
	10×104 t	20×104 t	30×104 t
建设规模10×104 t	100	100	100	100
建设规模20×104 t	0	300	300	0
建设规模30×104 t	－300	150	600	－300
max{最小效益}=max{100，0，－300}				100
优选的决策方案				建设规模10×104 t

表4.10  水泥厂规模决策表（三）               单位：万元

	可能增加的年需求量			效益期望值
	10×104 t	20×104 t	30×104 t
建设规模10×104 t	100	100	100	100
建设规模20×104 t	0	300	300	200
建设规模30×104  t	－300	150	600	150
平均概率	1/3	1/3	1/3	——
max{最大效益}=max{100，200，150}				200
优选的决策方案				建设规模20×104 t

例 4.6  某建筑企业在制定五年规划时，面临三种选择：扩大生产、新建企业、承包给工人生产。该企业生产的产品由于市场价格变动，利润也不相同。根据市场预测，五年内产品价格高、中、低的可能性分别是0.3，0.5，0.2，计算五年内的效益值如表4.12所示，问应采取哪一种方案决策。

表4.12  某企业未来五年各方案的效益表                单位：万元

	价         格
	高（0.3）	中（0.5）	低（0.2）
扩   建	60	35	-30
新   建	75	40	-45
承   包	70	40	-30

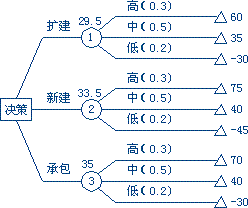
图4.1    某企业经营方案决策树

解：第1步，画出决策树（图4.1）。

第2步，计算各点的期望值： 点①：60×0.3 + 35×0.5 +（－30）× 0.2 = 29.5， 点②：75×0.3 + 40×0.5 +（－45）× 0.2 = 33.5， 点③：70×0.3 + 40×0.5 +（－30）× 0.2 = 35． 并将各期望值填在对应的节点上。

第三步选定方案。比较①、②、③点上的期望值，由于max{29.5, 33.5, 35}=35，留下期望值最大的点③一枝即为优选的决策方案。因此合理的决策应该是实行承包。