三角形边的关系说课稿

《三角形边的关系》说课稿
一、说教材
说课内容：人教版义务教育课程标准实验教科书《数学》第八册第82页例3——三角形边的关系。
三角形边的关系这一内容是新教材新增加的内容，并安排在第二学段。通过这一内容的学习，使学生在已经建立三角形概念的基础上，进一步深化理解三角形的组成特征，加深学生对三角形的认识，同时，也为以后学习三角形与四边形及其他多边形的联系与区别打下基础。
根据新课标的精神，要改变学生学习的方式，让学生经历“数学化”、“做数学”等过程，并注重与生活实际紧密联系，学有价值的数学。根据这一教学内容在教材中所处的地位与作用，以及新课标的要求，我认为设计这节课的理念是：活动参与、自主建构，联系生活、应用数学。
（一）教学目标
1．通过创设问题情景、直观演示、观察比较，初步感知三角形边的关系，体验学数学的乐趣；
2．通过实践操作、猜想验证、合作探究，算一算、比一比，经历发现“三角形任意两边的和大于第三边”这一性质的活动过程，发展空间观念，培养逻辑思维能力，体验“做数学”的成功；
3．运用“三角形任意两边的和大于第三边”的性质，解决生活中的实际问题。
（二）教学重点
1．引导发现不能摆成三角形的原因，并探讨能摆成三角形的边的性质。
2．理解、掌握“三角形任意两边之和大于第三边”的性质。
（三）教学难点
引导探索三角形的边的关系，并发现“三角形任意两边的和大于第三边”的性质。
二、说教法和学法
在“活动参与、自主建构，联系生活、运用数学”的设计理念指导下，我的教学思路是：问题引领、动手操作、合作探究规律，并在解决生活实际问题中促进每一位学生获得不同的发展。
（一）创设问题情景，激发学生学习兴趣
根据四年级学生的认知规律，我先给学生创设情景，引起悬念，激发学生学习数学的兴趣。让学生通过多媒体课件，直观感知三角形边的关系。
（二）动手操作、合作探究、自主建构数学规律
新课标强调要从学生已有的生活经验出发，自主地建构数学知识。因此我有意安排了三个层次的操作活动，提高学生的逻辑思维能力：
第一层次是动手操作，发现问题；
第二层次是小组合作，探究规律；
第三层次是推广验证，得出结论。
（三）关注学生生成，加强信息反馈
“关注学生生成，加强信息反馈”是我这节课实施时的最大特色，也是我教学的一贯风格。课堂上，学生小组的合作交流、自主的实验验证、互动评价等形式多样的活动，让我有充分的时空去关注学生的动态生成，多方面的深入了解学生的真实思维水平，及时点拨，使学生思维的空间在探索学习中得到有效拓展。
（四）联系生活，体会数学应用价值
数学《课程标准》指出“学生只有将数学与生活联系起来，才能够切实体会到数学的应用价值，学习数学的积极性才能够真正被激发”。因此，我将有意识地引导学生从数学的角度，应用所学的知识“三角形任意两边的和大于第三边”去解决生活中实际问题，让学生学有价值的数学。
三．说教学程序设计
依据我教学设计的理念、教学的设计思路，我的教学流程大致分为四个步骤。
（一）、联系生活、设疑引趣、提出问题
（二）、动手操作，合作探究，发现规律
（1）、动手操作，发现问题
（2）、小组合作，探究规律
（3）、推广验证，得出结论
（三）、深化认知，联系实际，拓展应用
（1）、基本练习，形成技能
（2）、发展练习，提高能力
（3）、拓展练习，灵活应用
（四）、整体回顾，总结评价，布置作业
（一）联系生活、设疑引趣、提出问题。

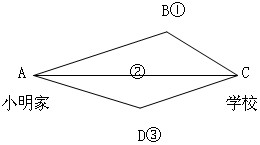
1．创设问题情景
（1）小明今天晚起床了，眼看上学快迟到了。这里有三条路线，你们猜猜小明走哪条路能最快到达学校？（学生回答）
（课件显示：小明以相同速度同时走这三条路线的不同结果）
（2）小明为什么走这条路最近？
揭示课题：三角形边的关系（并板书）
2．复习铺垫引疑
（1）什么样的图形是三角形？（由三条线段围成的图形叫做三角形）
（2）过渡：那是否三条线段就一定能围成三角形呢？
（二）动手操作，合作探究，发现规律
1．动手实验操作、填写数据
实验要求：四人小组每人拿一套小棒摆三角形，看看能不能摆成三角形。小棒长度分别为（1）6、7、8 （2）4、5、9 （3）3、6、10 （4）2、8、9
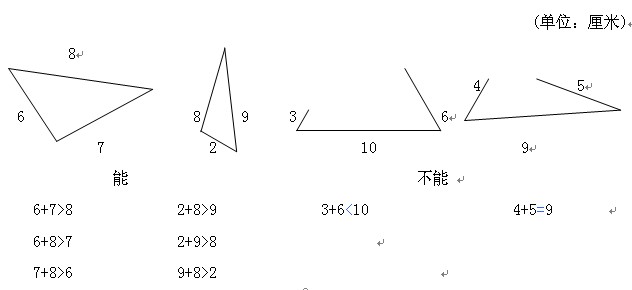
学生试摆的结果我以这4种情况作为代表： （单位：厘米）
 

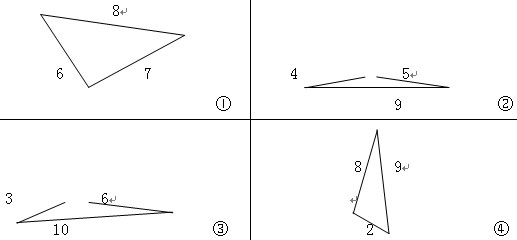
汇报操作结果（①④能摆成、②③不能摆成）（师根据学生的反馈在黑板上贴图形）。
师：为什么②③不能摆成呢？（小组讨论：学生说出两种情况）
为什么②③不能摆成呢？
原来三角形两条边的和与第三条边存在着一定的关系。那怎样的3条小棒才能围成三角形呢？
你能否通过计算来发现这一规律？

2．小组合作、合情推理，发现规律
（1）根据数据，学生小组合作，观察、计算、比较、分析能与不能的情况，把你小组的发现填写在表格内。
发给学生探究表：（数据由学生填写）

（2）师根据生汇报进行板书：
能 不能
6+7>8 2+8>9 3+6<10 4+5=9
6+8>7 2+9>8
7+8>6 8+9>2
根据三角形其中两边的长度和与第三边的长度比较，你有什么发现？
小结：原来只要其中两边长度的和小于或等于第三边，都不能围成三角形。只有当每两条边长度的和大于第三边，才能摆成三角形。也就是说：三角形任意两边的和大于第三边。
板书：三角形任意两边的和大于第三边。（齐读）
3．验证三角形边的关系在三角形中的普遍性。
（1）再次质疑、提出问题
师：是不是对于每个三角形来说，任意两边的和都大于第三边呢？
（2）动手操作、再次验证
通过量一量、算一算、比一比课前自定边长做的三角形：如在钉子板围的、纸上画的、用小棒搭的或用纸折的等，进行验证）。
4．回应引入
利用“三角形任意两边的和大于第三边”的性质解析情景问题。
5．看书质疑
（三）深化认知，联系实际，拓展应用。
1．基础练习：
在能拼成三角形的各组小棒下面画“√”。（单位：厘米）
1）

          3
              4
                  5  （ ）
2）

          3
          3
          3  （ ）
3）

          3
          3
                  5   （ ）
4）

        2
                      6
        2        （ ）

2．发展练习
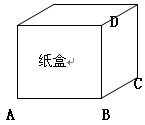
D 有一个正方体的纸盒，两只爬得同样快的蚂蚁分别从A点和C点出发，要吃放在D点上的糖。甲蚂蚁说：“我的路线是
C 经过B点，再到D点。”乙蚂蚁说：“我直接从C点到D点”。
A B 哪只蚂蚁能最快吃到糖？
 

› 三角形边的关系评课稿

› 三角形边的关系说课稿